Perseids ISS Telstar

One of the benefits of living in the boondocks is the minimisation of artificial light, so we're well placed for star-gazing.  The pretensions of the Celtic Tiger still linger in the desire to floodlight your dwelling to show how big it is and our neighbour across the valley has unfortunately signed up to this sect.  Nevertheless it's waaaay better than Dublin, let alone Los Angeles or London.  So last night I went up behind the house about 11 o'clock and lay out on the grass to watch the Perseids meteor shower.  It's not as exciting as Grand Theft Auto but it's worth doing because it's a natural wonder and rather wonderful for that.

So I was trying not to fall asleep - it was way past my bedtime and 'events' were only coming in every 2-3 minutes - when I saw a very bright light flickering through the trees as it lumbered in from the West. There's a LOT of crap endlessly circling our Earth and if you look up for longer than the time it takes to tweet about it you'll see that the night sky is busy. But the International Space Station is by far the biggest and brightest, and a check later with the Astronomy Ireland website said that the ISS had passed across Ireland at 2303hrs.  It was almost as exciting as 8-year-old me seeing Telstar bippling across the sky in the freezing winter of 1962/3 when there were so few artificial satellites that their appearance was listed in the newspaper under the weather report.  Cue The Tornadoes.

Puzzle time: 
IF
the Earth is 8000km in diameter 
ANDIF
the ISS orbits 400km above the surface
ANDIF
you have an unobstructed horizon and no clouds
ANDIF
the cosmonauts are clipping along at 7.7km/s (that's just under 30,000km/h)
How long will the ISS be visible as it passes overhead?
Answers on a postcard!  Answers added 20/Aug/13 below the fold:


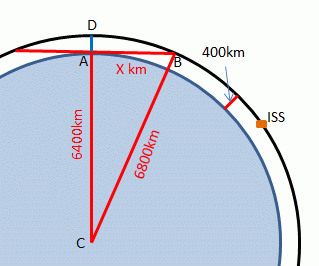
10 minutes! This is the kind of puzzle that brings up (bloooargh)  a lot of elementary maths that is half remembered from primary school.  Trigonometry.  S=O/H; C=A/H; T=O/A.  Pythagoras.  Thales' theorem: inscribed angles subtended by a diameter are always right.  It was wracking ma heid until I drew it out, thinking that if I mapped it to scale I could just measure the arc.  It was hard to find a compass to draw an accurate circle in our home-education household.  But as soon as it was drawn:

it was obvious that Pythogoras and his hypotenuse would do the trick. AB^2 = BC^2 – AC^2 = 2300km. So the distance from horizon to horizon is 4600km which is probably accurate enough. But you can do another Pythogorean calc to make it a better approximation: BD^2 = AD^2 + AB^2 = 2334km and the arc = 4668km. The ISS travels at 7.7 km/s so is visible for about 10 min. You can cross-check this with trig. Cos(AC/BC) = 0.909 and if you whip that into http://www.wolframalpha.com/input/?i=cos^%28-1%29+0.909 you find that the angle is 24.62deg. So the arc is 24.62/360th of Pi * 13600km = 2350km so the arc is 4700km but the time is still 10 minutes. It’s silly to say 10.1 minutes as the first estimate and 10.2 minutes as the second because the ISS is not going directly overhead and the chord and arc will have a different length if viewed obliquely.And the true mean radius of the Earth is not a round 6400km but slightly less - 6375km.  And it's only in an ideal world that there are no trees, no clouds, no hills to obscure the horizon.