Geography 201

Today we tie up a loose end about the ISS and offer an explanatory of map of why, after endless rounds of playing Isn't Uncle Bob Clever, Geoguessr starts to seem samey.  Check out the other 39 maps on the same page - bri'nt!  And there's a nice post about exclaves and enclaves in Nor'n Ire''n' on the StrangeMaps site - can you be a separate country because you're the last Catholic on a Protestant street?  Ulster .ne. N.I. etc. in the comments

ANNyway, a tuthree days ago I posed a guesstimation conundrum about the visibility of the International Space Station which you must have a geek at the end of this post before going below the fold to see the answer.
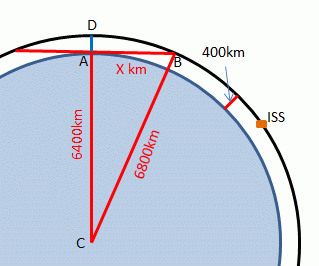
10 minutes! This is the kind of puzzle that brings up (bloooargh)  a lot of elementary maths that is half remembered from primary school.  Trigonometry.  S=O/H; C=A/H; T=O/A.  Pythagoras.  Thales' theorem: inscribed angles subtended by a diameter are always right.  It was wracking ma heid until I drew it out, thinking that if I mapped it to scale I could just measure the arc.  It was hard to find a compass to draw an accurate circle in our home-education household.  But as soon as it was drawn:

it was obvious that Pythogoras and his hypotenuse would do the trick. AB^2 = BC^2 – AC^2 = 2300km. So the distance from horizon to horizon is 4600km which is probably accurate enough. But you can do another Pythogorean calc to make it a better approximation: BD^2 = AD^2 + AB^2 = 2334km and the arc = 4668km. The ISS travels at 7.7 km/s so is visible for about 10 min. You can cross-check this with trig. Cos(AC/BC) = 0.909 and if you whip that into http://www.wolframalpha.com/input/?i=cos^%28-1%29+0.909 you find that the angle is 24.62deg. So the arc is 24.62/360th of Pi * 13600km = 2350km so the arc is 4700km but the time is still 10 minutes. It’s silly to say 10.1 minutes as the first estimate and 10.2 minutes as the second because the ISS is not going directly overhead and the chord and arc will have a different length if viewed obliquely.And the true mean radius of the Earth is not a round 6400km but slightly less - 6375km.  And it's only in an ideal world that there are no trees, no clouds, no hills to obscure the horizon.